一般にバッテンで曲線を回すと、端点近傍は直線となっている。この範囲を減らすには端点近くに点を押えるとよい。5点で曲線を押えようとすれば、点は図2.2.14のような配置であろう。

図2.2.14

さて、このように点列の接続で表わされた空間曲線の実長は、どのように求めるか。

直線の実長を求めた方法を拡大するのである。点のある位置ごとに平行平面を想定し、平面間スペースの上に、各点間の「落ち」を目盛って行き、その目盛った点を接続すれば、それが実長の曲線となる（図2.2.15）。「落ち」はその平行平面上の投影曲線上で拾い、求める実長も点列接続曲線上で求める。

直線の実長の説明では、その端点を含む二平面と、「落ち」（その投影線）を含んで二平面に直交する第三の平面を想定し、この直線を含んだ第三の面を作画して実長を捉えた。この第三の面は、空間曲線ではどうなるか。これは平面ではなく、空間曲線を含み、点列ごとの平行平面に直交する曲面になるのである。この曲面を平面上に展開したのが、実長曲線の作画と捉えれば、直線の場合と全く同じ方法であると理解できる。

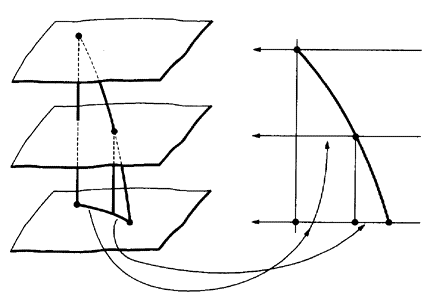
図2.2.15

次は、曲線/曲面での角度である。幾何学では、交点における各々の曲線/曲面の接線のなす角であるが、さきに見たように点列で表現される曲線は、接線の意味があるほどの確かさでは、船体曲面もそれから派生する曲線も捉えていない。

さきに直線/平面の角度の説明で、展開に角度は使わない方がよい、としたが、曲線/曲面では、使ってはならない、としておく。

現図展開とは関係ないが、外板曲面上で求めて現場に渡す必要のある角度がある。ついでだから、その考え方を示しておく。

・取付け度：組立時に使用する角度自在金の足の当たる点を求めて出す（図2.2.16）。曲り外板が逆反りのときはどうするか。下げ振り度は、そのためにある。

・曲げ型当て度：曲り外板では、当て位置と見透し線を押えるのが第一義であり、当て度は参考なので、曲面上に直線を近似させる。ここらの詳しい論議は別途としておく。

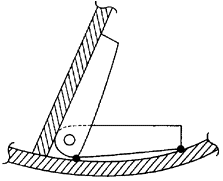
図2.2.16

前ページ　　　目次へ　　　次ページ